If you have been following our series of Trivia Crack scoring analyses, you may be wondering how we developed our estimates.  It’s actually an interesting process, and it plays into our strengths here at Corona Insights, of measuring a population when we can only gather data for a sample.  So let’s take a quick break from the scoring analyses and talk a little about how we did it.

The Challenges of Measuring

Trivia Crack offers six scores for each player, one each for history, geography, science, sports, arts, and entertainment.  Scores range from 0 to 100, and reflect the percentage of questions that a person has answered correctly.  We can also calculate a total score by adding the six scores together.

However, it’s not that easy.  We don’t have access to the master database, and there are four big challenges in measuring scores if your only way of gathering data is by playing the game.

  • First, Trivia Crack provides scores for individuals, but doesn’t provide scores for the whole population. So we had to sample the population by playing games against random opponents.  Lots and lots of games against random opponents.  We gathered data for 432 opponents, which meant that we had access to the answering patterns for more than 440,000 questions.  That part was pretty fun.
  • Second, Trivia Crack is actually two similar games. There’s a one on one matchup against a single random opponent, and there are challenge matches where you play against nine opponents at once.  It’s easier to sample data in the challenge matches because you gather data nine times faster.  But are the players and scores different?
  • Third, we have a classic statistical problem of sample sizes and variance. If you only answer 1 question, it’s pretty easy to get a score of 100.  If you answer 10, it’s more difficult.  If you answer 1,000, it’s almost impossible.  So we needed to be sure that our analysis wasn’t tainted by this fact.
  • And finally, there’s a subtle but important complication. If you start a game and select a random opponent, you’re more likely to draw a person who plays often and has answered more questions.  So when we start a game and randomly draw an opponent, we’re not drawing a true sample of players.  We’re overrepresenting players who play more often.  Those players may have higher scores because they’re good at the game and having fun, or they may have lower scores because it’s hard to maintain consistent high scores over time.  We have to figure this out and statistically correct for it if it turns out that scores are higher or lower for more frequent players.

So How Did We Measure?

First off, we played a lot of games, always against random opponents, and then we entered their scores into a database.  That part was easy.  We also set a rule that we would not include a person’s score in the analysis if they hadn’t answered at least 300 questions.  While somewhat arbitrary as a threshold, this requirement eliminated a lot of the random variation that comes when people answer only a few questions.  We eventually gathered data on 392 players, which was enough to do a strong analysis.

The statistical corrections were a little more complicated.  First, we tackled the issue of the two types of games.  We gathered from both group challenges and individual matchups, and found that there is indeed a difference in scoring.  Players in challenge matches tend to have lower scores, possibly because there’s a time pressure in challenge matches that doesn’t exist in one on one matches.  So we made some statistical corrections to assume that a player splits his or her time evenly between challenge matches and one on one matches.

The last correction is a little more complex.  We did an analysis and found out that the most frequent players tend to have higher scores.  In general, every 1,000 questions answered equates to about a 1 point gain in each of the categories, or 6 points in total.  This can throw our numbers off because we’re more likely to encounter high-frequency players when we draw a random opponent, which will then overestimate the scoring of a typical player.

To correct for this, we statistically weighted our data to account for the fact that more frequent players are overrepresented.  The scores of each player in our database were weighted according to the inverse of the number of questions they’d answered in their Trivia Crack career.  Players who have answered more questions are more likely to be randomly drawn because they play more often, so we weighted them down in inverse proportion to the number of questions they have answered over time.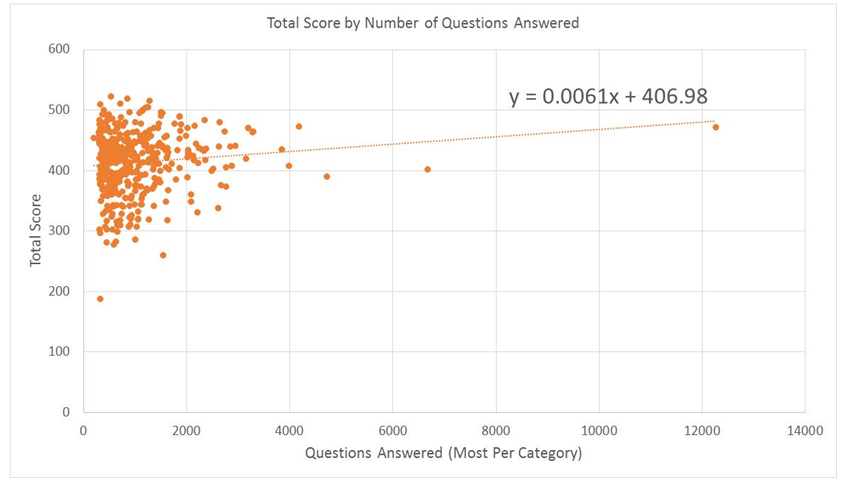Total Score by Number of Questions Answered

In summary, it’s a more complicated analysis than simply drawing random opponents and looking at their scores.  But we developed some systems to do these corrections, and that made the process easier.  And by the way, kudos to the fellow in our sample who had answered over 12,000 questions per category.

One thing you will notice in all of the category analyses is a bit of a jagged pattern – a sawtooth.  We figure that those would smooth out if we gathered information on a lot more scores, but hey, we have to earn a living.  We can’t just be playing games all day.

So enough about methodology.  Let’s get back to the scoring.

Check out our next scoring analysis, the fun topic of Entertainment questions.